Since it got cold and snowy, I’ve been walking to work and wearing snow pants to deal with the weather.  Today, for the first time that I remember, I apparently got the snow pants off the hook by the front door and put them with my coat to get ready and had no memory of doing it.

This is a habitual sequence I’ve been doing since it got cold and apparently it’s now automated enough that I can do it without leaving an explicit memory trace.  How many days ago did the temperature drop and I start this habit?  Just about 50.  That was also just about how many days of biking it took for me to lock the bike with no memory of it later.

50 times through a sequence to get to automaticity.  Seems like a perfectly reasonable hypothesis.

Back from vacation today and greeted by a Chicago Tribune headline with a beautiful example of how to badly confuse people with numbers. Now I wish I hadn’t skipped my “how to lie with statistics” lecture in 205 last quarter since this is the main trick I talk about. The short form: if somebody is explaining something to you as a percent change on a rate statistic, hold on to your wallet because you are probably being conned.

The headline was: “75% tax increase proposed” which on the online version is, “Democratic lawmakers push 75% state income tax increase” which at least makes it clear it’s about state income tax while also tipping the political-point being made by the right-leaning trib (Dems raise your taxes, beware!).

I wonder how many people read the headline and think the state is proposing a 75% income tax rate?  Nobody is used to thinking of percent change on a rate and they often confuse which rate is being affected.  If you know something about Illinois state taxes, you know the current state income tax rate is 3%.  The current proposal is to raise that to 5.25%.  Is that a 75% increase or a 2.25% increase?  Yes to both actually and how you describe it depends on how you want people to react to the statement.

You can’t really win here.  If you describe the rate increase as a 2.25% increase, most readers won’t realize that if they paid $1,000 in state tax last year, they will have to pay $1,750 this year — which is a bigger difference than “+2.25%” implies.  OTOH, a “75% increase” is going to be read as a 75% rate by a decent fraction of the readers who are probably going to think the gov’t is potentially about to confiscate virtually all their wages.

Innumeracy is a problem.  Given how many otherwise smart people either avoid math or are bad at it, it’s not at all clear how one would effectively communicate basic facts about budgetary issues, medical risk factors or other kinds of rate information.

BTW, one of the games you are playing with the rate-of-rate statement like “75% increase” is that the rate being changed isn’t in the headline.  I guessed it was the state income tax, but I actually looked at the article to see if they meant sales tax.  In IL, sales taxes can run to 11.5% and a +75% rate increase would be pretty noticeable.  Base rates are important.  “Doubling your risk of heart attack” isn’t so bad if your base rate is 1 in a million.  It’s pretty grim if it’s one in 10, though.

We are thinking of skill learning as depending on sequence learning in which a set of actions are chained together into a fluid, well-performed execution sequence.  In SISL, like Guitar Hero, the interface steps you through a specific sequence (repeatedly) and you become better at the sequence.  The William James idea of water carving an increasingly deeper trench captures the idea, although you have to assume deeper = better here.

That’s all well and good for skills you learn by stepping through the goal sequence and can improve by simple repetition.  But a friend recently suggested to me that in some skills, there are a lot of possible paths and some of these are inefficient meaning that practicing them won’t help much.  You’ll get better at a  bad strategy, but you’ll never become expert.  He proposed that golf is an example.  There are too many ways to swing a club to hit a ball and just hitting it repeatedly willy-nilly won’t make you a scratch golfer.

I think this is the idea behind why Ward & Ericsson talk about “deliberate practice.”  Either through external coaching or explicit learning and top-down control, you need to guide yourself through the right sequence and then you can practice it.  In addition to the right/wrong strategy, this might also reduce variance helpfully by guiding you to repeat the same sequence.

The “problem space” concept is a way or representing possible strategic paths from your start to your goal state.  In SISL & GH, the path is highly linear.  In a game like chess, you have up to dozens of possible moves at each state, so if you try to map out the possible paths, you get a very bushy problem space.  The degree to which you need “deliberate practice” or coaching or top-down deduction to guide your sequence learning is likely determined by how bushy the problem space is — how easy is it to find the ideal path to solution.

This may not sound very random, but wait: Starcraft 2!

Starcarft 2 is the latest version of the real-time strategy multi-player competition video game from Blizzard.  I’m currently playing it with my boys and therefore have the opportunity to subjectively observe the skill learning process.  Because it’s competitive and you play against other players, Blizzard works very hard to rate your play and try to match you up with appropriate opposition.  Since we are hoping to learn, we expect to see this reflected in increasingly difficult opponents (and increasing rating).

It is also obvious that pure willy-nilly practice does not guarantee robust learning in SC2.  There are tons of people in the lowest division (with me) with records like 500 wins, 500 losses.  One thousand games and they haven’t been promoted yet.  Why not?  Probably because it’s a fantastically complicated problem space with dozens of major strategic decisions, timing decisions, adjustment decisions.  Without some top-down control or coaching, it’s going to take roughly forever to hone the correct sequences.

Coaching?  In a video game?  Yes, and here’s where it gets really random.  SC2 is nearly a major sport in Korea, but gamers all over the world are following the Global Starcraft League Season 3 competition in which some of the best players in the world compete for about ~$175,000 in prizes.

One way they cover the prize money is that they charge to watch the replays with expert commentary at GOMtv (http://www.gomtv.net/2010gslopens3/).  Why pay to see the experts play explained?  So we can get that top-down control.  And also root for Jinro, the one non-Korean in the final field of 32 (which the American commentators seem to do).

Commented SC2 games are available in a number of places including youtube, e.g., http://www.youtube.com/user/ArtosisTV.

An embedded example:

Sherman’s Lagoon is doing a series on Guitar Hero.  This is today’s (11/30/10) from the Chicago Tribune.

From a few weeks ago, but it’s still funny to me.

It’d be interesting to find out what sort of percentage of students take advantage of paper-writing mills.

Either way, this is a pretty interesting article from someone who works at one.

http://chronicle.com/article/The-Shadow-Scholar/125329/

For some reason, I decided that my Research Methods class would gain by a discussion of the phenomenon of regression to the mean. In hindsight, it didn’t connect to the rest of the material that well. I think I was just captured by this quote from Danny Kahneman. I’m excepting it here from wikipedia (Regression toward the mean) which is excerpting it from his biography, although I saw some part of the quote elsewhere that made me go looking for the original.

The first part of the quote is actually about a curious consequence of the regression to the mean phenomenon:

I had the most satisfying Eureka experience of my career while attempting to teach flight instructors that praise is more effective than punishment for promoting skill-learning. When I had finished my enthusiastic speech, one of the most seasoned instructors in the audience raised his hand and made his own short speech, which began by conceding that positive reinforcement might be good for the birds, but went on to deny that it was optimal for flight cadets. He said, “On many occasions I have praised flight cadets for clean execution of some aerobatic maneuver, and in general when they try it again, they do worse. On the other hand, I have often screamed at cadets for bad execution, and in general they do better the next time. So please don’t tell us that reinforcement works and punishment does not, because the opposite is the case.”

The second part is what really stuck in my mind, though (this is still Kahneman reporting the incident in his bio):

This was a joyous moment, in which I understood an important truth about the world: because we tend to reward others when they do well and punish them when they do badly, and because there is regression to the mean, it is part of the human condition that we are statistically punished for rewarding others and rewarded for punishing them. I immediately arranged a demonstration in which each participant tossed two coins at a target behind his back, without any feedback. We measured the distances from the target and could see that those who had done best the first time had mostly deteriorated on their second try, and vice versa. But I knew that this demonstration would not undo the effects of lifelong exposure to a perverse contingency.

What he’s describing here is one of the dark sides of automatic, statistical habit learning.  There might be anomalous contingencies in the real work (e.g., yelling at people seems to work due to regression to the mean) and we pick up these tendencies and they become ingrained due to our automatic statistical learning mechanisms.  Implicit stereotypes (bias, prejudice) probably occur by roughly the same mechanism.

P.S. There’s some sort of clever joke/pun about regression, habits and being mean that could be derived from the title, but I don’t quite see how to make it pithy, so it is left as an exercise for the reader.

Extra randomness today.  I had seen this awhile ago and decided to go find it again on youubte.  It’s a 2m completely pointless sequence of actions practiced and near-perfected by WGN news anchors to pass the time during commercial breaks.

I meant to count the actions sequenced, but I always get distracted by wondering why this is entertaining — to watch, but also to perform.  I suppose it’s dance-like in ways.  It’s obviously taken a lot of practice and why? Where’s the reward?

It seems like dreaming and memory are still huge topics in popular science. I guess we can thank Hollywood (Eternal Sunshine, Inception). The article is about epileptic patients with intracranial electrodes and how they have particular MTL firing when viewing particular pictures. However, as it progresses across the internet and is re-written, some of the small details are lost. Like the fact that the brain recordings are done with electrodes implanted into someone’s brain. I think we have a few years before we get to Matrix-level human brain to computer interfacing.

Either way, it’s sort of amusing to see how removed from the science the articles get as you progress from source to source. I dub it the “Science of Kevin Bacon.”

It goes from a Nature article, to the BBC news, to a gawker.com blog. If I can find someone crosslink to Gawker, and subsequently later reach six degrees of separation, that would be awesome.

http://www.nature.com/nature/journal/v467/n7319/full/nature09510.html

http://www.bbc.co.uk/news/science-environment-11635625

http://gawker.com/5675295/scientist-says-a-dream-tivo-is-possible

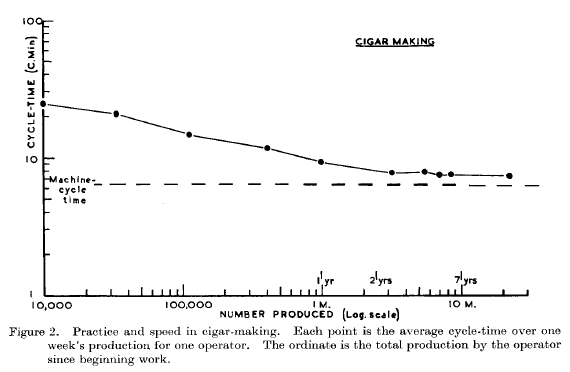
There’s a famous old data set on skill learning & expertise on workers rolling cigars that is used as an example of trying to understand the underlying skill learning rate (and therefore process).  I was reminded of the data by Scott Grafton last week and thought I’d dig it up for the lab website.  I found the article:

Crossman, E. R. F. W. A theory of the acquisition of speed-skill. Ergonomics 2, 153–166 (1959).

But it turns out our library subscription of the journal Ergonomics only goes back to 1997.  I’ve put in a ILL request for the article and will update this with a learning curve picture when it arrives.

The data are sometimes used as part of a math-psych debate about whether skill learning produces an “exponential” shaped learning curve or a “power law” shaped learning curve.  These are the mathematical forms of these curves:

Power: E(RT)  = A + B * N^-β

Exponential: E(RT) = A + Be^-(α N)

E(RT) (expected value of RT at this point in training) is the data fit as a function of free parameters: A, B plus the learning rate parameters (beta for power, alpha for exponential).  A reflects a fit to initial performance, B is the initial estimated gain rate.  For both learning functions, you can fit skill learning curves pretty well with algorithms that look for the best fit from your observed data to reasonable values of the 3 parameters.

One challenge is that data are noisy and both curve forms are pretty good at fitting pretty much any initial learning curve (that is negatively accelerated, that is, you get less improvement per time of practice as you get more practice). They start to separate at very high levels of practice, partly because the power law curve doesn’t have an asymptote.  It just keeps getting better forever.  That makes the curious prediction that you can always keep getting better with more practice — but is this true?  Doesn’t there have to be a physical limit to the rate your muscles can contract and relax?

Which brings us back to cigars.  In that 1959 study, some of the experts had been doing cigar rolling daily for more than 7 years, rolling more than 10 million cigars — and they were still learning, they were still making incremental gains.  I’ve heard that there was some evidence of an asymptote (floor) in gains, but it turned out to be a function of the machine, not the ability of learning in the expert users.

There’s a good paper, Heathcote, Brown & Mewhort (2000), that argues for exponential learning curves over power-law learning curves.  There’s a wee bit of math involved, but I think I’ll make decoding this kind of analysis a focus of the math/computation grad seminar this Spring.  Not everybody loves papers with formulas, greek letters and calculus, but always remember: Math is Your Friend.

Update: Cigar figure